〇. 前言
由于种种原因,CSAPP 应该安排上日程了。
很感谢学姐能在高考结束后给我推荐了这么好的计算机入门书,惭愧的是看的太慢了,一个月只推了一章的内容…
希望开学之后能收收心,把速度调快一点,整本书尽量能在四个月内结束吧。
第一章《系统漫游》
本章作为引子,主要是讲了一些计算机相关的概念,笼统概括如下:
-
源程序在编译过程中经历四个阶段(预处理,编译,汇编,链接),最终形成了可执行目标程序(第 3 章)。
-
系统硬件组成及存储器层次结构。
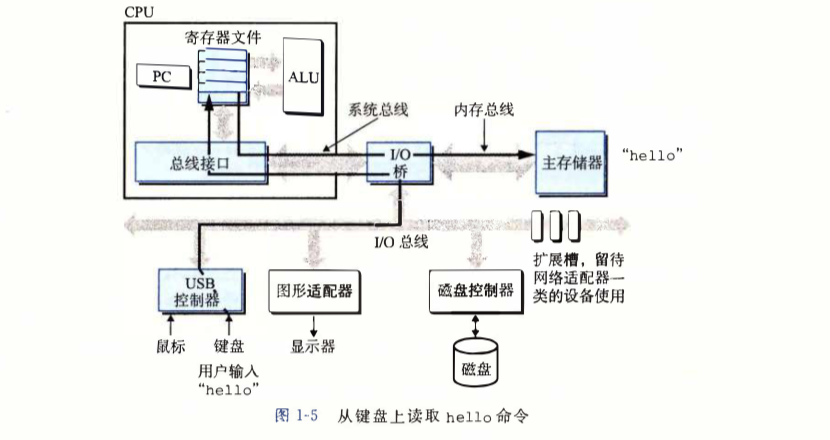
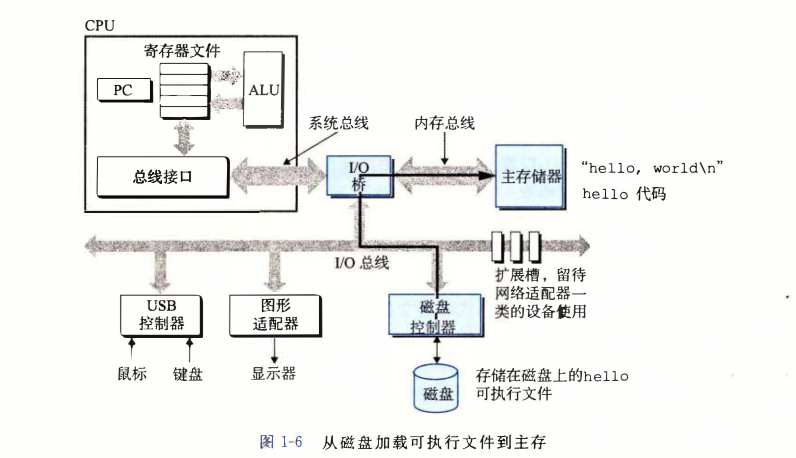
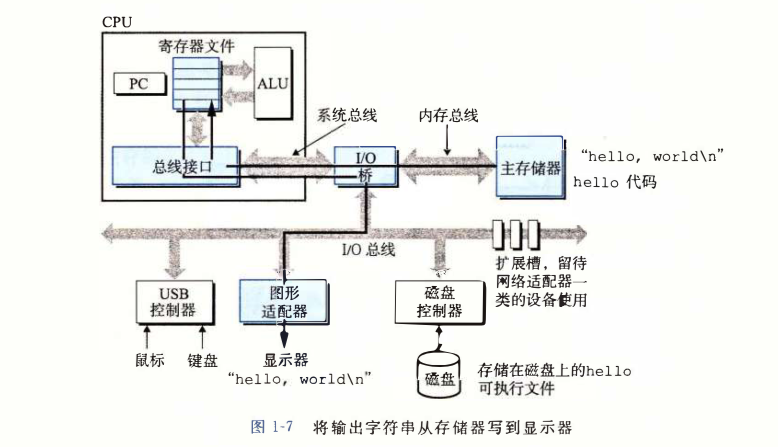
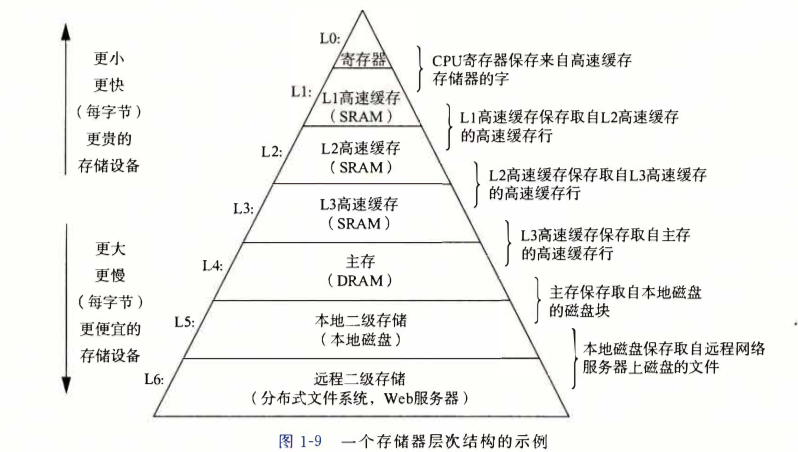
-
“三个抽象”
这个还是要提一嘴,抽象是 CS 中非常重要的概念。子曰:“CS 领域内没有什么问题,是不能通过增加一层抽象来解决的。”
首先我们得明确操作系统的概念:本质上,操作系统是链接应用程序 与 硬件之间插入的一层软件。
我们知道操作系统有两个基本功能:(1)防止硬件被恶意滥用;(2)向应用程序提供简单一致的机制来控制低级硬件设备。
“三个抽象” 正是操作系统为了实现这两个基本功能引入的简化模型,即:
(1)文件是对 I/O 设备的抽象表示(第 10 章);
(2)虚拟内存是对主机与磁盘 IO 设备的抽象表示(第 8 章);
(3)进程是对处理器,内存及 IO 设备的抽象表示(第 8,12 章)。
- 并发与并行
为了让计算机“更快更高更强”,处理器在不断迭代的过程中往往从两方面提升其能力:并发与并行。具体来说实现的方法为:多线程 or 超线程并发;指令级并行与单指令多数据并行。
- 虚拟机是对于计算机的抽象。
第二章《程序结构与执行》
主要讲了无符号编码,补码,浮点数编码及其性质。
-
字,字节与地址
-
位级运算,逻辑运算与移位运算
其中右移有两种:对于无符号数采用逻辑位移,符号数采用算数位移。原因知道补码表示后显然。
- 无符号数编码及补码
要注意范围(溢出)问题,扩展位问题,加减法运算溢出判定,乘法溢出判定
- IEEE浮点表示
一个二进制浮点数由符号位,阶码 (exp) ,尾数 (frac)组成的,公式 ,其中 。
编码组合共有三种情况:
- 规格化:exp 非 0 ,也非全 1,此时公式里的
- 非规格化:exp=0,,可以表示出 0
- exp=1 且 frac=0 时表示为无穷大;exp=1 且 frac 非 0 返回 NaN .
最后讲了个浮点数舍入的问题,遵循的是向偶数舍入 。
2.60:十六进制表示
大多数计算机使用 8 位的块,或者宇节( byte) ,作为最小的可寻址的内存单位。
一个十六机制数字可以表示 4 个二进制数字,从而简化了表示。
若想将一个无符号数中的某一字节替换为字节 b ,只需先把对应位置的字节标 0 ,再移位即可。
具体地说,(x & ~((0xff)<<(8*i)) | ( b<<(8*i) ) 。
2.63:算术右移与逻辑右移
对于无符号编码与补码,右移有两个不同的机制:前者用前缀 0 补全,后者用最高有效位补全。
unsigned srl(unsigned x,int k) {
unsigned xsra = (int) x>>k; int all_bits=sizeof(int)<<3;
int t=(~0) ^ ( (1 << (all_bits-k)) -1);
return ( xsra & (~t) );
/* ↑只改变最高字节,设0 */
}
int sra(int x,int k) {
int xsrl = (unsigned) x>>k; int all_bits=sizeof(int)<<3;
bool check = x & ( 1<<(all_bits-1) ); //判断符号位
int t=(~0) ^ ((check << (all_bits-k) ) -1);
//若符号位为 0,t = 0 ;若符号位为 1,t将高于 k 位自动填充 1.
return ( xsrl | t );
}
2.66:移位小技巧
给定一个整型数,将除最高有效位的 1 设置为 0。
通过倍增移位,可将其转换为0001111… ;
可保证即使只有最高位为 1 也能满足条件。
int left_one(unsigned x)
{
x |= x>>1; x |= x>>2; x |= x>>4; x |= x>>8; x |= x>>16;
// return (x+1)>>1; 这样操作会爆UMAX!!!
return x ^ (x>>1);
}
2.67:移位小贴士
当你对一个 int 向左移位 32 位,相当于没移。
2.73:最值溢出问题 及 小技巧
代码给出两个判定 int 溢出的方法,但题目要求不给使用条件语句。
我们可以利用逻辑运算符性质:若第一个参数运算值可以得出结果,便不会执行第二个。
int saturating_add(int x,int y)
{
int sum = x+y;
bool ext_p = x>0 && y>0 && sum<=0;
bool ext_m = x<0 && y<0 && sum>=0;
ext_p && (sum=INT_MAX) || ext_m && (sum=INT_MIN);
//这句话非常有意思,代替了一个 if
return sum;
}
2.75:补码与无符号数的转换
位值相同的 补码 与 无符号数 之间的关系是:
因此设无符号数,补码,则
取 32~63 位,因此最后一项可略去。
unsigned unsigned_high_prod(unsigned x,unsigned y)
{ return sign_high_prod(x,y) + (int)(x>>31)*y + (int)(y>>31)*x;}
2.78:补码除法
补码除法遵循向下舍入,当为负数时便十分不合常理,因此需要修正。
通常的,我们通过设置偏置值来抵消影响: 对于 , 令 即可。
简要证明:设 ,原式
若 。则后面一项为 0 ;若非 0 ,则后面一项为 1 。
int div_power2(int x,int k)
{
bool is_neg = x & INT_MIN; // 判负
( is_neg && (x+=(1<<k)-1) );
return (x>>k);
}
2.89:浮点数精度问题
按理说单精度浮点数最大可表示到,但是会存在极大的精度损失。
若要连续的表示出整型数,最大范围只有 。
为什么?因为 float 的尾数部分只有 n=23.
2.97:综合型大杂烩
题意:
给定一个正整数 i ,求出他的浮点数表示 f。
分析:
我们大致的思路是:(1)确定符号位;(2)确定最高有效位的位置,从而设置阶码;(3)剩余位置即为尾码,通过移位进行修正。
我们还发现了许多坑点:
(1)确定符号位后取绝对值,但如果是 INT_MIN,由补码性质可知没有对应的正数。
因此我们对此进行特判。
(2)取最高有效位可参照 2.66 的做法。阶码设置为 ,其中
(3)尾码非常之恶心,因为我们可以取到 int 一切实数,而大部分都存在精度损失。
而浮点数编码的舍入满足向偶数舍入,我们只需模拟此过程即可。
float_bits float_i2f(int i)
{
unsigned sig = (i<0), exp, frac;
if (i<0) {
if (i == INT_MIN) {//特判
exp = 127 + 31; frac = 0;
return sig << 31 | exp << 23 | frac;
}
i = -i;
} //(1)
int max_bit = length(i); exp = max_bit + 127; //(2)
unsigned rest = i ^ (1 << max_bit) ;
if (max_bit <= 23) // 精度范围内
frac = rest << (23 - max_bit);
else { //精度外,进行舍入
int overflow = 23 - max_bit;
int round_mid = 1 << (overflow-1),
round_num = rest & ((unsigned)-1 >>(32- overflow)) ;
frac = rest >> overflow;
if (round_num > round_mid ||
(round_mid == round_num && (frac & 0x1) ==1) ) frac += 1;
//若大于一半,或等于一半且向偶数舍入时进位
}
return sig << 31 | exp << 23 | frac;
}