一些早就知道却没用过 或是 从来没听说过可能会有用 的优化方式。
一. 编译器 优化方式:
-
减小计算量:乘法比加法来的时间慢,能转化成加法的尽量不用乘法。
-
多维数组引用:由于行优先的原则,一行元素总是在内存上连续的,而连续内存引用更快。所以遍历多维数组的时候应该以之前的维数为基遍历,切忌越维遍历。
-
循环调用函数:对于遍历字符串时,如果判断条件写成
i<strlen(s)就会爆炸;原因是strlen()本身是一个 线性函数,所以遍历算法大致上 是 O(n^2) 的。
编译器不会优化该问题的原因是:在遍历字符串内部时我们可能会改变字符串长度,所以编译器会很小心的对待长度,每次都会重新计算一遍;
另一个原因是,strlen 函数在 string.h 库里,它可能会在编译之后才在链接阶段被使用,编译器不能对 strlen 功能做出判断。
- Memory Matters(这个不知道):
void sum_row(double *a, double *b, int n) {
for (int i = 0; i < n; i++) {
b[i] = 0;
for (int j = 0; j < n; j++)
b[i] += a[i * n + j];
}
}
假设我写了这么一个程序,很直白就是说;但是他的汇编代码十分不正常:编译器首先从内存读出 b[i] 存在寄存器 %xmm0,再将 a[i*n+j] 加到寄存器中,又重新把值赋给内存。 得到了如下汇编代码:
0x0000000000401594 <+52>: lea (%r11,%rax,1),%r9d // hold a_i address
0x0000000000401598 <+56>: movslq %r9d,%r9
0x000000000040159b <+59>: movsd (%r10),%xmm0 // b_i into register
0x00000000004015a0 <+64>: addsd (%rcx,%r9,8),%xmm0 // add a_i
0x00000000004015a6 <+70>: movsd %xmm0,(%r10) // register into b_i
如此在内存与寄存器传送数据,极大地拖慢了程序运行速度。 怎么会是呢?原来,有一种可能就是 ,即 B 数组覆盖(或替身)A 中的某一行,这被称作 内存别名使用。如果改变了 B 数组,同时也改变了 A 中的值,导致求和结果的不同。
因此,编译器无法否定内存别名使用的情况,这需要我们引入局部变量,先将求和结果存储于 val 结尾在赋值,就可以防止类似反复调用内存的问题。
优化后的汇编代码片段如下:
0x0000000000401590 <+48>: lea (%r10,%rax,1),%r9d //hold a_i address
0x0000000000401594 <+52>: movslq %r9d,%r9
0x0000000000401597 <+55>: addsd (%rcx,%r9,8),%xmm0 // add a_i into val
0x000000000040159d <+61>: add $0x1,%eax
这便减少了内存调用,加快了程序运行速率。
二. 指令级别的并行程序:
1. 理解现代处理器:
这些优化是基于处理器所实现的,可以在任何机器上进行。
在微处理器层面上,我们有两种下界描述其最大性能:
- 延迟界限:当一系列操作按照顺序执行时,指令级并行所带来的限制要求下一条指令开始前目前的指令必须结束;
- 吞吐量界限:代表处理器功能单元的原始计算能力。
超标量处理器允许其在每个时钟周期执行多个 乱序 操作;整个设计有两个主要部分:指令控制单元(ICU) 以及 执行单元(EU),区别于按序流水线相比,乱序处理器能达到更高的指令集并行度。
ICU 从 指令缓存 中读取指令并译码,再将其发给 EU 操作。
面对选择分支时,我们通常使用 预测分支 的技术,猜测程序是否选择分支,并通过预测分支的目标地址,使用 投机执行 的技术,取出对应的指令提前译码;如果之后确认预测错误,则返回到分支点的状态。
2. 功能单元
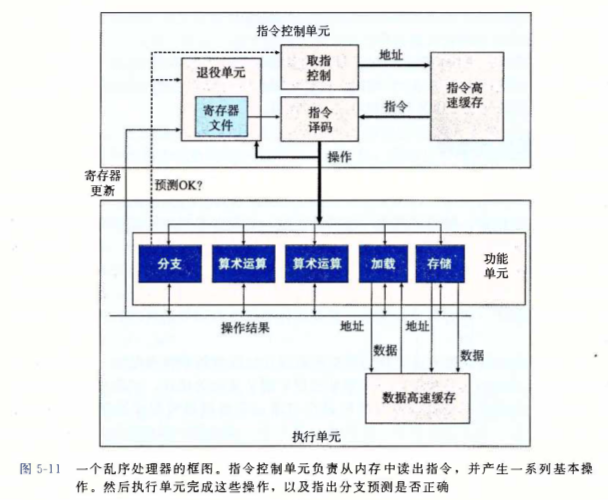
一个功能单元应该能完成多项任务,例如从处理器将数据写到内存的存储单元,不仅应该具备写入的功能,也应做到地址运算。
功能单元的性能由以下数值刻画:一是延迟(latency),表示完成运算的总时间;二是发射时间,表示两同类型的运算之间所需的最小时钟周期;最后一个是容量(capacity),表示能执行概运算的功能单元的数量。
我们引入一个叫 CPE 的指标,判断进行一次计算所需要的 时钟周期 是多少。我们所需要优化的就是单次运算的 CPE。在编译层面上我们优化后至多可降到:

整型乘法之所以需要三个时钟周期是取决于现代 CPU 的设计方法。假设指令序列是内存上连续的一串,CPU 会提前读取一串指令再将它们分开,一些无关联的指令就可以同时执行(利用指令的并行性),这可以极大加快计算机的处理速度,我们称为 超标量乱序执行。
同时,功能单元可以利用 流水线 技术进行优化。实际上,对于一个乘法器它被分成了三个阶段,一次乘法运算需要三个时钟周期,那么三次乘法运算就需要九个时钟周期。所幸的是,利用流水线优化,我们可以压缩到7个甚至更少(这依赖于指令的并行性)。如下图:
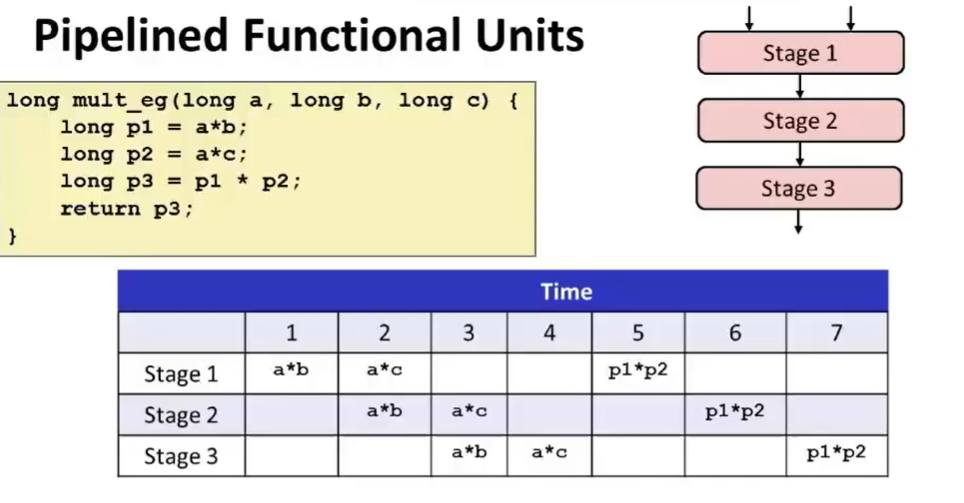
3. 循环展开 及 提高并行性
循环展开 是指通过增加每次迭代计算的元素数量从而减少迭代次数的技巧。例如如果同时处理前置和的两个元素,使得迭代数量减半,其中计算循环索引和条件计算的时间便大大减小了。如此操作可以使得 CPE 逼近延迟界限。我们称其为 2*1展开。

由于我们将答案始终存储在单独的变量中,而在之前的计算完成之前都不能计算其新值。这也是为何突破不了延迟界限的原因。
因此,我们可以将答案就拆开,acc0 表示偶数的累计值, acc1表示奇数的累计值,最后处理落单的元素、将其合并为完整的答案。我们称其为 2*2 循环展开。

总的来说,重新组合变换能减少计算中关键路径上的操作数量。由于浮点数不符合结合律,大多数编译器不会对浮点运算做重新结合。