《动手学强化学习》学习笔记【一】

第一节 初探强化学习

1. 概念

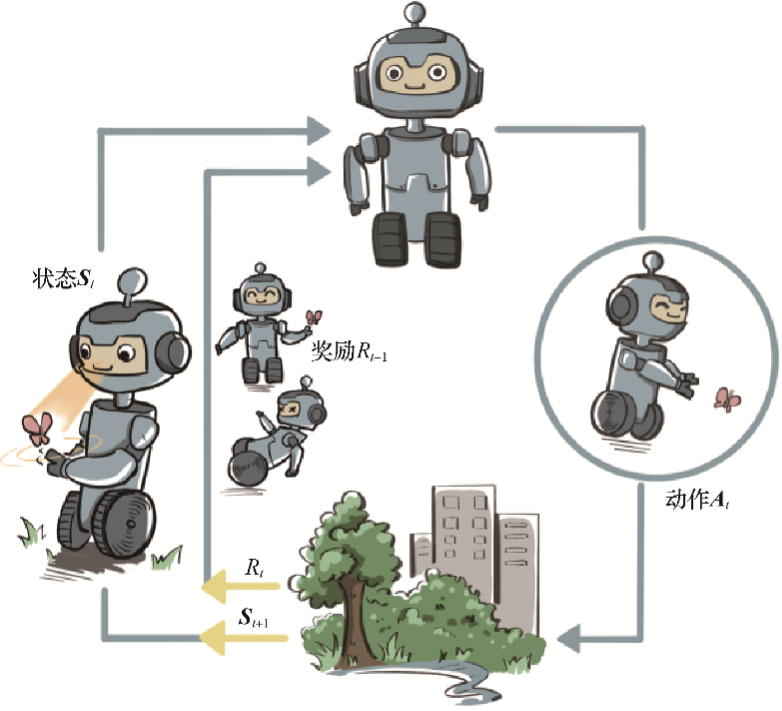
广泛地讲，强化学习是机器通过与环境交互来实现目标的一种计算方法。 机器和环境的一轮交互是指，机器在环境的一个状态下做一个动作决策，把这个动作作用到环境当中，这个环境发生相应的改变并且将相应的奖励反馈和下一轮状态传回机器。这种交互是迭代进行的，机器的目标是最大化在多轮交互过程中获得的累积奖励的期望。

强化学习用智能体（agent）这个概念来表示做决策的机器。相比于有监督学习中的“模型”，强化学习中的“智能体”强调机器不但可以感知周围的环境信息，还可以通过做决策来直接改变这个环境，而不只是给出一些预测信号。

这里，智能体有3种关键要素，即感知、决策和奖励。

• 感知。智能体在某种程度上感知环境的状态，从而知道自己所处的现状。例如，下围棋的智能体感知当前的棋盘情况；无人车感知周围道路的车辆、行人和红绿灯等情况。
• 智能体根据当前的状态，计算出达到目标需要采取的动作的过程叫作决策。例如，针对当前的棋盘决定下一颗落子的位置；针对当前的路况，无人车计算出方向盘的角度和刹车、油门的力度。
• 奖励。环境根据状态和智能体采取的动作，产生一个标量信号作为奖励反馈。这个标量信号衡量智能体这一轮动作的好坏。例如，围棋博弈是否胜利；无人车是否安全、平稳且快速地行驶。【最大化累积奖励期望】是智能体提升策略的目标，也是衡量智能体策略好坏的关键指标。

【面向决策任务的强化学习】和【面向预测任务的监督学习】在形式上是有不少区别的：

• 首先，决策任务往往涉及多轮交互，即序贯决策；而预测任务总是单轮的独立任务。如果决策也是单轮的，那么它可以转化为“判别最优动作”的预测任务。
• 其次，因为决策任务是多轮的，智能体就需要在每轮做决策时考虑未来环境相应的改变，所以当前轮带来最大奖励反馈的动作，在长期来看并不一定是最优的。

2. 环境

生活中几乎所有的环境（或者说，系统）都在进行演变，例如一座城市的交通、一片湖中的生态、一场足球比赛、一个星系等，这在数学和物理中往往用随机过程来刻画。对于一个随机过程，其最关键的要素就是状态以及状态转移的条件概率分布。如果在环境这样一个自身演变的随机过程中加入一个外来的干扰因素，即智能体的动作，那么环境的下一刻状态的概率分布将由当前状态和智能体的动作来共同决定，用最简单的数学公式表示则是：

$下一状态 \sim P(⋅ ∣ 当前状态，智能体的动作)$

根据上式可知，智能体决策的动作作用到环境中，使得环境发生相应的状态改变，而智能体接下来则需要在新的状态下进一步给出决策。每一轮状态转移都伴随着两方面的随机性：一是智能体决策的动作的随机性，二是环境基于当前状态和智能体动作来采样下一刻状态的随机性。

3. 目标

智能体和环境每次进行交互时，环境会产生相应的奖励信号，其往往由实数标量来表示。整个交互过程的每一轮获得的奖励信号可以进行累加，形成智能体的整体回报（return）。根据环境的动态性我们可以知道，即使环境和智能体策略不变，智能体和环境交互产生的结果也很可能是不同的，对应获得的回报也会不同。因此，在强化学习中，我们关注回报的期望，并将其定义为价值（value），这就是强化学习中智能体学习的优化目标。

价值的计算有些复杂，因为需要对交互过程中每一轮智能体采取动作的概率分布和环境相应的状态转移的概率分布做积分运算。强化学习和有监督学习的学习目标其实是一致的，即在某个数据分布下优化一个分数值的期望。

对于一般的监督学习任务，我们的目标是找到一个最优的模型函数，使其在训练数据集上最小化一个给定的损失函数。在训练数据独立同分布的假设下，这个优化目标表示最小化模型在整个数据分布上的泛化误差（generalization error）

$最优模型 = \arg\min_{模型} E_{(特征，标签)\sim数据分布} [损失函数(标签，模型(特征))]$

奖励函数是对于未来累积奖励的预测，评估给定策略下状态的好坏。相比之下，强化学习任务的最终优化目标是最大化智能体策略在和动态环境交互过程中的价值，而策略的价值可以等价转换成奖励函数在策略的占用度量上的期望，即：

$最优策略=\arg\max_{策略}E_{(状态,动作)\sim策略的占用度量}[奖励函数(状态,动作)]$

二者优化的途径是不同的，监督学习直接通过优化模型对于数据特征的输出来优化目标，即修改目标函数而数据分布不变；强化学习则通过改变策略来调整智能体和环境交互数据的分布，进而优化目标，修改数据分布而目标函数不变。

但现在 RLFT 真的只能微调（顶多几个 epoch 就结束了），不管有没有收敛都得结束，再调下去原来的能力也要丢失了。目前仍缺少一个长期的、稳定的 RLFT 方法。

4. 数据

在强化学习中，数据是在智能体与环境交互的过程中得到的。如果智能体不采取某个决策动作，那么该动作对应的数据就永远无法被观测到，所以当前智能体的训练数据来自之前智能体的决策结果。智能体的策略不同，与环境交互所产生的数据分布就不同。

具体而言，强化学习中有一个关于数据分布的概念，叫作占用度量（occupancy measure），其具体的数学定义和性质会在第3章讨论，在这里我们只做简要的陈述：归一化的占用度量用于衡量在一个智能体决策与一个动态环境的交互过程中，采样到一个具体的状态动作对（state-action pair）的概率分布。

占用度量有一个很重要的性质：**给定两个策略及其与一个动态环境交互得到的两个占用度量，那么当且仅当这两个占用度量相同时，这两个策略相同。**也就是说，如果一个智能体的策略有所改变，那么它和环境交互得到的占用度量也会相应改变。

根据占用度量这一重要的性质，我们可以领悟到强化学习本质的思维方式。

• **强化学习的策略在训练中会不断更新，其对应的数据分布（即占用度量）也会相应地改变。**因此，强化学习的一大难点就在于，智能体看到的数据分布是随着智能体的学习而不断发生改变的。
• 由于奖励建立在状态动作对之上，策略对应的价值其实就是占用度量下对应的奖励的期望，因此寻找最优策略对应着寻找最优占用度量。

第二节 多臂老虎机

有一个拥有 $T$ 根拉杆的老虎机，拉动每一根拉杆都对应一个关于奖励的概率分布 $R$。我们每次拉动其中一根拉杆，就可以从该拉杆对应的奖励概率分布中获得一个奖励 $r$。我们在各根拉杆的奖励概率分布未知的情况下从头开始尝试，目标是在操作 $T$ 次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的，因此我们需要在 “探索拉杆的获奖概率” 和 “根据经验选择获奖最多的拉杆” 中进行权衡。

有关多臂老虎机提出了算法的累积懊悔理论，$\epsilon$-贪心算法、上置信界算法和汤普森采样算法在多臂老虎机问题中十分常用，其中上置信界算法和汤普森采样方法均能保证对数的渐进最优累积懊悔。多臂老虎机问题与强化学习的一大区别在于其与环境的交互并不会改变环境，即多臂老虎机的每次交互的结果和以往的动作无关，所以可看作无状态的强化学习。第 3 章将开始在有状态的环境下讨论强化学习，即马尔可夫决策过程。